Fungsi

 Sejarah Fungsi

Galileo Galilei (1564-1642) merupakan salah satu astronom terkenal dari Italia yang dikenal luas dengan penemuannya tentang hubungan yang sangat teratur antara tinggi suatu benda yang dijatuhkan dengan waktu tempuhnya menuju tanah.

Konsep “fungsi” terdapat hampir dalam setiap cabang matematika, sehingga merupakan suatu yang sangat penting artinya dan banyak sekali kegunaannya. Akan tetapi pengertian dalam matematika agak berbeda dengan pengertian dalam kehidupan sehari-hari.Dalam pengertian sehari-hari, “fungsi” adalah guna atau manfaat.

Kata fungsi dalam matematika sebagaimana diperkenalkan oleh Leibniz (1646-1716) terlihat di atas digunakan untuk menyatakan suatu hubungan atau kaitan yang khas antara dua himpunan. Mengingat konsep fungsi menyangkut hubungan atau kaitan dari dua himpunan, maka disini kita awali dulu pembicaraan kita mengenai fungsi dengan hubungan atau relasi antara dua himpunan.

1.       Pengertian Fungsi

       Adalah relasi khusus yang memasangkan setiap anggota A dengan tepat satu anggota B.

2.       Notasi dan Nilai Fungsi

        f : x à y atau f : x à f(x)

        Dibaca : fungsi f memetakan x anggota A ke y anggota B.

3.     Menyatakan Fungsi dalam Diagram Panah, Cartesius, dan Himpunan Pasangan Berurutan

            Contoh:

             Jika diketahui

•      Dalam diagram panah, diagram Cartesius, himpunan pasangan berurutan dapat disajikan sebagai  berikut:

1.          Diagram Panah

                  

   2.   Diagram Cartesius 

          3.       Himpunan pasangan berurutan

                R = {(0, 1), (1, 2), (2, 3), (5, 6)}

4.  Menentukan Rumus Fungsi Jika Nilainya Diketahui

     Diketahui f fungsi linear dengan f(0) = -5 dan f(-2) = -9. Tentukan bentuk fungsi f(x).

 ü  Penyelesaian :

      Karena f fungsi linear maka f(x) = ax + b.

      Dengan demikian diperoleh

      f(0) = -5

      f(0) = a(0) + b  = -5

                  0 + b =-5

                        b = -5

      f(-2) = -9

      f(-2) = a(-2) + b = -9

            -2a + (-5) = -9

                          a = 2

     Jadi fungsi yang dimaksud adalah f(x) = ax + b = 2x – 5

 5.     Menghitung Nilai Perubahan Fungsi Jika Nilai Variabelnya Berubah

Misalkan fungsi f ditentukan oleh f : x à 5x + 3 dengan domain {x/-1 ≤ x ≤ 3, x є bilangan bulat}. Jika variabel x diubah menjadi x + 3, maka nilai perubahan fungsi dari f(x) dan f(x+3) yaitu selisih dari keduanya.

Diketahui f(x)     = 5x + 3, maka

     f(x+3)           = 5 (x+3) +3

                          = 5x + 15 +3

                          = 5x + 18

Nilai perubahan fungsi dari f(x) menjadi f(x+3) adalah

                                      f(x+3)-f(x)           = (5x + 18) – (5x + 3)

                                                                                = 15.

6.      Grafik Fungsi (Pemetaan)

Grafik suatu pemetaan (fungsi) adalah bentuk diagram Cartesius dari suatu pemetaan (fungsi). Perhatikan contoh berikut:

Gambarlah grafik fungsi f : x à x+3 dengan domain

a: { x | 0 ≤ x ≤ 8, x € bilangan bulat },

b: { x | 0 ≤ x ≤ 8, x € real }.

Penyelesaian:

Untuk memudahkan menggambar grafik fungsi f : x Ià x+3, kita buat terlebih dahulu tabel yang 

memenuhi fungsi tersebut, sehingga diperoleh koordinat titik-titik yang memenuhi.

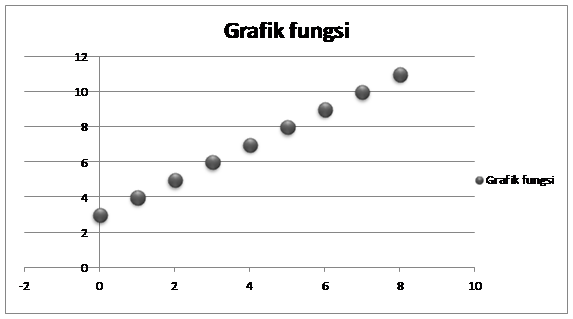
Gambar grafik dari tabel di atas:

Berdasarkan grafik fungsi f : x à x + 3 dengan domain {x | 0 ≤ x ≤ 8, x € bilangan real} berupa

titik-titik noktah saja,akan tetapi bagaimana jika titik-tik tersebut dihubungkan?

Berdasarkan grafik fungsi f : x à x + 3 dengan domain {x | 0 ≤ x ≤ 8, x € bilangan real} jika titik-titiknya dihubungkan ternyata akan membuat garis

ü  Mengapa demikian?

      Fungsi f pada himpunan bilangan real (R) yang ditentukan oleh rumus f(x) = ax + b dengan a, b € R dan a ≠ 0 disebut fungsi linear. Grafik fungsi linear berupa suatu garis lurus dengan persamaan y = ax + b.

      Dari kedua grafik fungsi di atas, dapat ditarik kesimpulan bahwa jika domain dan kodomainya hanya terbatas pada himpunan bilangan bulat rangenya dapat digambarkan dengan noktah-noktah saja namun jika domain dan kodomainnya diperluas pada himpunan bilangan riil, rangenya dapat ditunjukkan dengan garis yang melalui noktah-noktah tersebut.

       

Perhatikan deretan rumah di suatu kompleks rumah (perumahan). Setiap rumah memiliki nomor rumah tertentu yang berbeda dengan nomor rumah yang lain. Mungkinkah satu rumah memiliki dua nomor rumah? Atau mungkinkah dua rumah memiliki nomor rumah yang sama? Tentu saja jawabannya tidak. Keadaan sebuah rumah memiliki satu nomor rumah atau satu nomor rumah dimiliki oleh sebuah rumah dikatakan sebagai korespondensi satu-satu.

 Contoh lain:

Jika ibukota propinsi yang terdapat di pulau Kalimantan dikelompokkan dalam himpunan A dan propinsi yang terdapat di pulau Kalimantan dikelompokkan dalam himpunan B, maka relasi ibukota propinsi dari himpunan A ke himpunan B dinyatakan dalam diagram panah sebagai berikut.

A = { Banjarmasin, Samarinda, Palangkaraya, Pontianak }

B = { Kalimantan selatan, Kalimantan Timur, Kalimantan Tengah, Kalimantan Barat }

Sebaliknya apabila kita membuat relasi ibukotanya adalah dari himpunan B ke himpunan A, maka diagram panahnya adalah sebagai berikut.

Kedua relasi di atas adalah fungsi karena fungsi  dengan relasi “ibukota propinsi” memetakan himpunan A kepada himpunan B, sebaliknya fungsi dengan relasi “ibukotanya adalah” memetakan himpunan B kepada himpunan A. Pemetaan yang bersifat bolak-balik atau dua arah ini disebut korespondensi satu-satu.

Dari uraian di atas maka dapat kita simpulkan bahwa Korespondensi satu-satu adalah fungsi yang memetakan anggota dari himpunan A dan B, dimana semua anggota A dan B dapat dipasangkan sedemikian sehingga setiap anggota A berpasangan dengan tepat satu anggota B dan setiap anggota B berpasangan dengan tepat satu anggota A. Jadi, banyak anggota himpunan A dan B harus sama atau n(A) = n(B). banyak korespondensi satu-satu yang mungkin antara himpunan A dan B adalah n! = n x (n – 1) x (n – 2) x ... x 3 x 2 x 1. n! dibaca : n faktorial.

sumber: file pribadi